1993: Stochastic volatility model by Heston
The Heston model is a useful model for simulating stochastic volatility and its effect on the potential paths an asset can take over the life of an option.
- Popular because of easy closed-form solution for European option pricing
- no risk of negative variances
- incorporation of leverage effect
This allows for more effective modeling than the Black-Scholes formula allows due to its restrictive assumption of constant volatility.
Heston Model SDE
The heston model is defined by a system of SDEs, to describe the movement of asset prices, where anasset’s price and volatility follow random, Brownian motion processes (this is under real world measure \(\mathbb{P}\)):
\(\large dS_t = \mu S_t dt + \sqrt{v_t}S_t dW^\mathbb{P}_{S,t}\)
\(\large dv_t = \kappa(\theta – v_t)dt +\sigma \sqrt{v_t} dW^\mathbb{P}_{v,t}\)
Where the variables are:
– \(\sigma\) volatility of volatility
– \(\theta\) long-term price variance
– \(\kappa\) rate of reversion to the long term price variance
– \(dW^\mathbb{P}_{S,t}\) Brownian motion of asset price
– \(dW^\mathbb{P}_{v,t}\) Brownian motion of asset’s price variance
– \(\rho^\mathbb{P}\) correlation between \(dW^\mathbb{P}_{S,t}\) and \(dW^\mathbb{P}_{v,t}\)
Dynamics under risk-neutral measure \(\mathbb{Q}\):
\(\large dS_t = r S_t dt + \sqrt{v_t}S_t dW^\mathbb{Q}_{S,t}\)
\(\large dv_t = \kappa^\mathbb{Q}(\theta^\mathbb{Q} – v_t)dt +\sigma^\mathbb{Q} \sqrt{v_t} dW^\mathbb{Q}_{v,t}\)
Heston Model for Monte Carlo Simulations
Obviously as discussed one of the nice things about the Heston model for European option prices is that there is a closed-form solution once you have the characteristic function. So discretisation of the SDE is not required for valuing a European option, however if you would like to value other option types with complex features using the Heston model than you can use the following code:
Euler Discretisation of SDEs
Great resource for explanation here: Euler and Milstein Discretization by Fabrice Douglas Rouah https://frouah.com/finance%20notes/Euler%20and%20Milstein%20Discretization.pdf
\(\Large S_{i+1} = S_i e^{(r-\frac{v_i}{2}) \Delta t + \sqrt{v_{i}}\Delta tW^\mathbb{Q}_{S,i+1}}\)
\(\large v_{i+1} = v_i + \kappa(\theta – v_t)\Delta t +\sigma \sqrt{v_i} \Delta t W^\mathbb{Q}_{v,i+1}\)
Import dependencies
import numpy as np import seaborn as sns import matplotlib.pyplot as plt from py_vollib_vectorized import vectorized_implied_volatility as implied_vol
Define Parameters
Here we just define the parameters of the model under risk-neutral dynamics, however in a following tutorial I will show how to calibrate Heston model parameters under risk-neutral dynamics to real option market prices.
# Parameters # simulation dependent S0 = 100.0 # asset price T = 1.0 # time in years r = 0.02 # risk-free rate N = 252 # number of time steps in simulation M = 1000 # number of simulations # Heston dependent parameters kappa = 3 # rate of mean reversion of variance under risk-neutral dynamics theta = 0.20**2 # long-term mean of variance under risk-neutral dynamics v0 = 0.25**2 # initial variance under risk-neutral dynamics rho = 0.7 # correlation between returns and variances under risk-neutral dynamics sigma = 0.6 # volatility of volatility theta, v0
Monte Carlo Simulation
Because we have a recursive function, we have to step through time within our simulation. However we can simulate the Brownian motions of the asset and variances outside of the for loop.
def heston_model_sim(S0, v0, rho, kappa, theta, sigma,T, N, M):
"""
Inputs:
- S0, v0: initial parameters for asset and variance
- rho : correlation between asset returns and variance
- kappa : rate of mean reversion in variance process
- theta : long-term mean of variance process
- sigma : vol of vol / volatility of variance process
- T : time of simulation
- N : number of time steps
- M : number of scenarios / simulations
Outputs:
- asset prices over time (numpy array)
- variance over time (numpy array)
"""
# initialise other parameters
dt = T/N
mu = np.array([0,0])
cov = np.array([[1,rho],
[rho,1]])
# arrays for storing prices and variances
S = np.full(shape=(N+1,M), fill_value=S0)
v = np.full(shape=(N+1,M), fill_value=v0)
# sampling correlated brownian motions under risk-neutral measure
Z = np.random.multivariate_normal(mu, cov, (N,M))
for i in range(1,N+1):
S[i] = S[i-1] * np.exp( (r - 0.5*v[i-1])*dt + np.sqrt(v[i-1] * dt) * Z[i-1,:,0] )
v[i] = np.maximum(v[i-1] + kappa*(theta-v[i-1])*dt + sigma*np.sqrt(v[i-1]*dt)*Z[i-1,:,1],0)
return S, v
rho_p = 0.98 rho_n = -0.98 S_p,v_p = heston_model_sim(S0, v0, rho_p, kappa, theta, sigma,T, N, M) S_n,v_n = heston_model_sim(S0, v0, rho_n, kappa, theta, sigma,T, N, M)
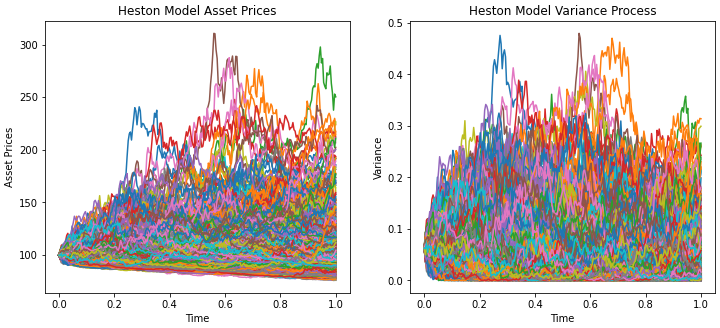
Plotting the asset prices and variance over time
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12,5))
time = np.linspace(0,T,N+1)
ax1.plot(time,S_p)
ax1.set_title('Heston Model Asset Prices')
ax1.set_xlabel('Time')
ax1.set_ylabel('Asset Prices')
ax2.plot(time,v_p)
ax2.set_title('Heston Model Variance Process')
ax2.set_xlabel('Time')
ax2.set_ylabel('Variance')
plt.show()
Asset price distribution with different correlations
# simulate gbm process at time T
gbm = S0*np.exp( (r - theta**2/2)*T + np.sqrt(theta)*np.sqrt(T)*np.random.normal(0,1,M) )
fig, ax = plt.subplots()
ax = sns.kdeplot(S_p[-1], label=r"$\rho= 0.98$", ax=ax)
ax = sns.kdeplot(S_n[-1], label=r"$\rho= -0.98$", ax=ax)
ax = sns.kdeplot(gbm, label="GBM", ax=ax)
plt.title(r'Asset Price Density under Heston Model')
plt.xlim([20, 180])
plt.xlabel('$S_T$')
plt.ylabel('Density')
plt.legend()
plt.show()

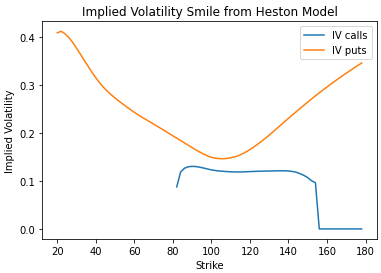
Capturing the Volatililty Smile in Option Pricing
rho = -0.7
S,v = heston_model_sim(S0, v0, rho, kappa, theta, sigma,T, N, M)
# Set strikes and complete MC option price for different strikes
K = np.arange(20,180,2)
puts = np.array([np.exp(-r*T)*np.mean(np.maximum(k-S,0)) for k in K])
calls = np.array([np.exp(-r*T)*np.mean(np.maximum(S-k,0)) for k in K])
put_ivs = implied_vol(puts, S0, K, T, r, flag='p', q=0, return_as='numpy', on_error='ignore')
call_ivs = implied_vol(calls, S0, K, T, r, flag='c', q=0, return_as='numpy')
plt.plot(K, call_ivs, label=r'IV calls')
plt.plot(K, put_ivs, label=r'IV puts')
plt.ylabel('Implied Volatility')
plt.xlabel('Strike')
plt.title('Implied Volatility Smile from Heston Model')
plt.legend()
plt.show()