Risk-Neutral Pricing of Weather Derivatives
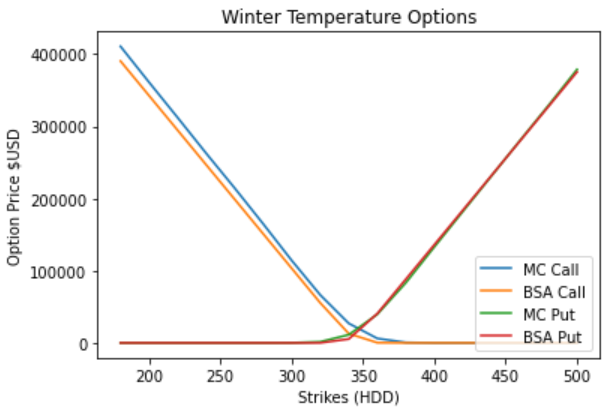
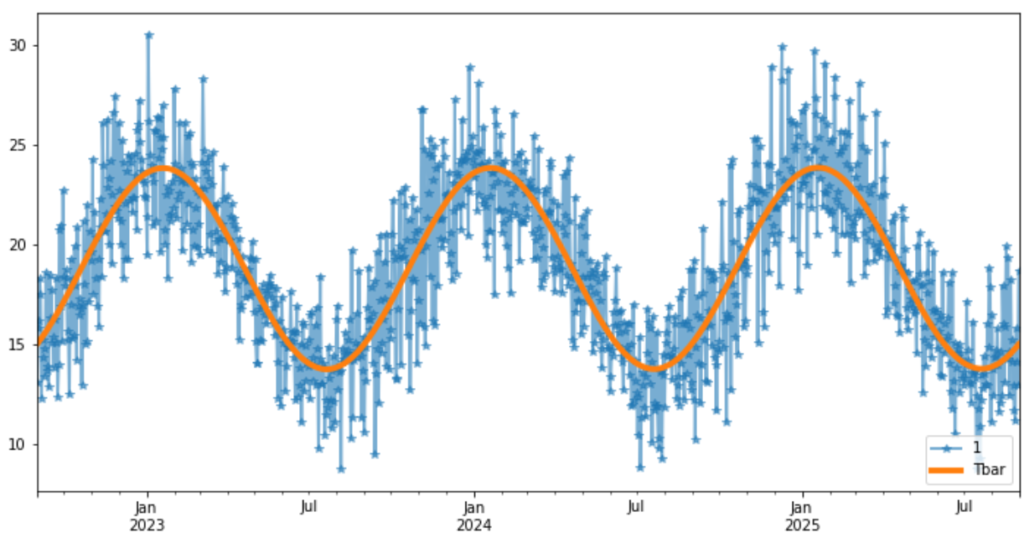
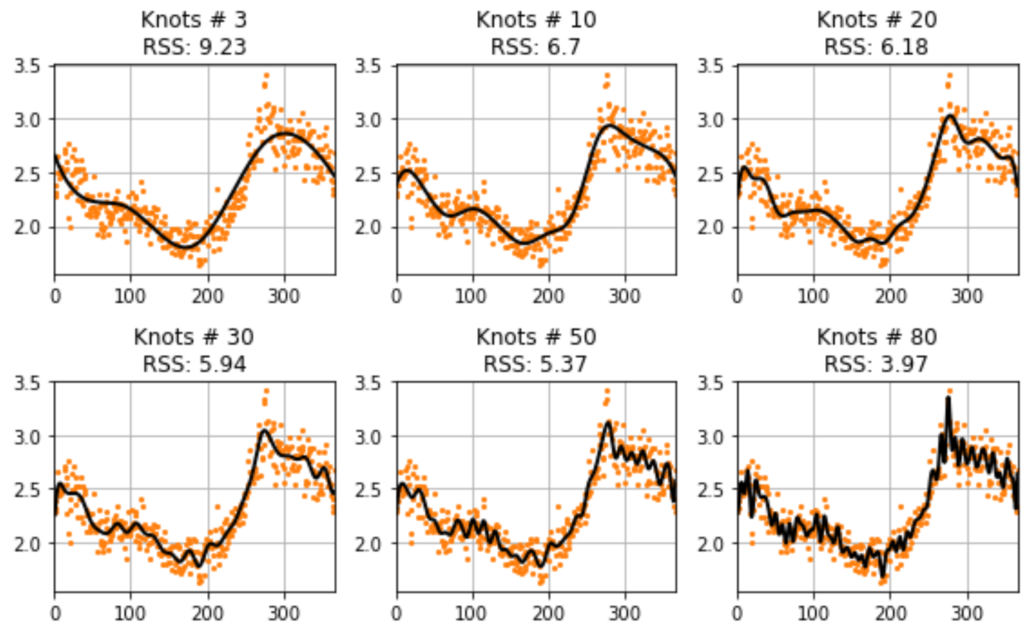
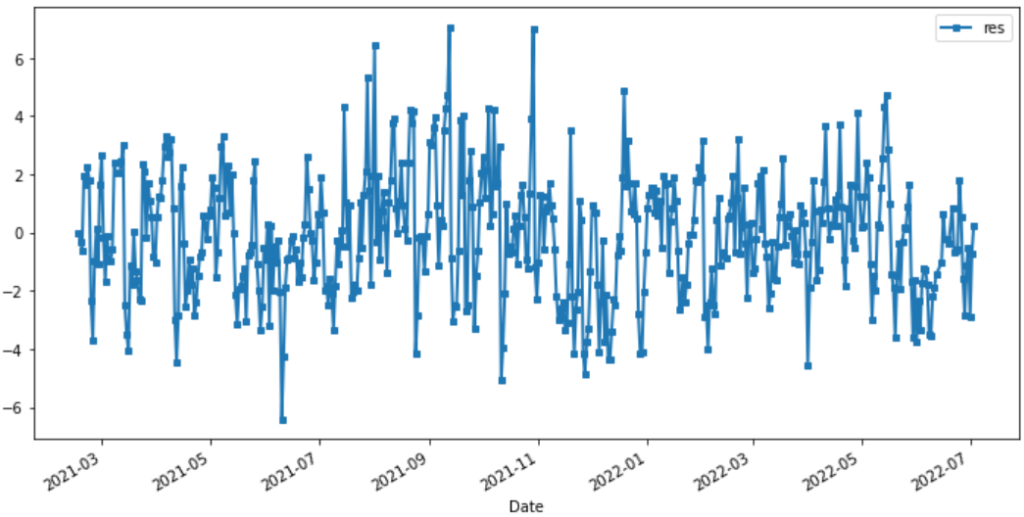
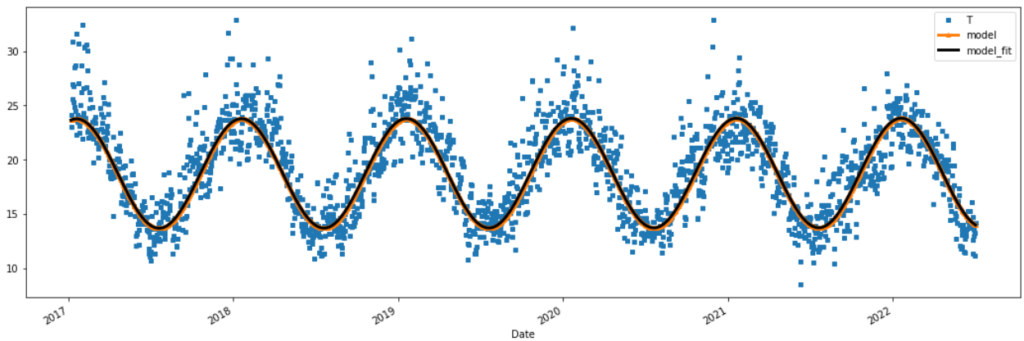
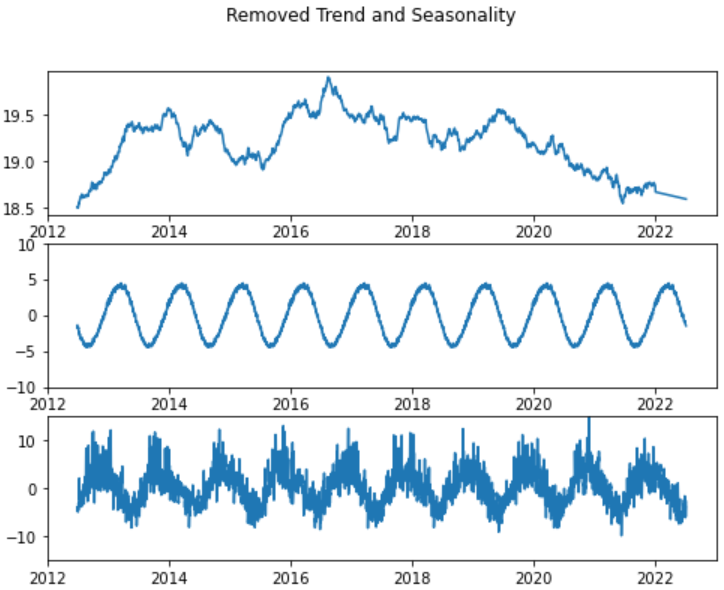
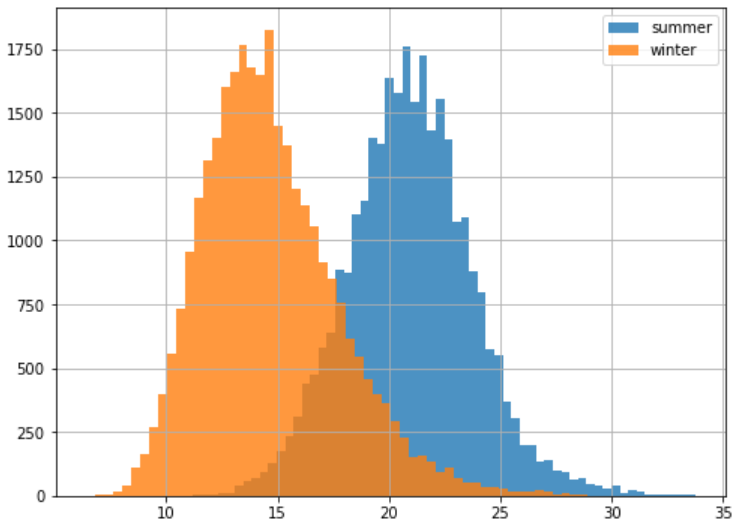
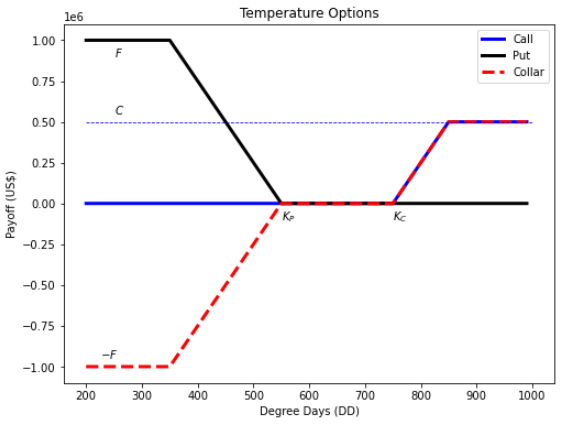
In this tutorial, we finally use the risk-neutral pricing methodology for valuation of our temperature options in python. In this online tutorial series dedicated to weather derivatives we have estimated the parameters of our modified mean-reverting Ornstein-Uhlenbeck process which defines our Temperature dynamics, and have now implemented different models for our time varying volatility. Now we move on to calculating option prices using both Monte Carlo simulation method under the risk neutral probability measure and an alternative black scholes like approximation for winter seasons!
Risk-Neutral Pricing of Weather Derivatives Read More »