Monte Carlo

The method of Importance Sampling involes a change of distribution using the Radon-Nikodym derivative. So we conductr a simulation under a new probability measure and then multiply by the ratio of the two probability density functions (the old over the new), or the Radon Nikodym derivative of one process with respect to the other.

In this tutorial we discuss Monte Carlo convergence and the difference between Pseudo-random numbers and Quasi-random numbers. In previous tutorials will discusses the benefits of combining Monte Carlo Variance Reduction techniques such as antithetic and control variate methods to reduce the standard error of our simulation.

We demonstrate the effectiveness of using quasi-random numbers by compaing the convergence on a pricing a European Call Option by monte carlo simulation using difference methods for creating pseudo and quasi-random variables.

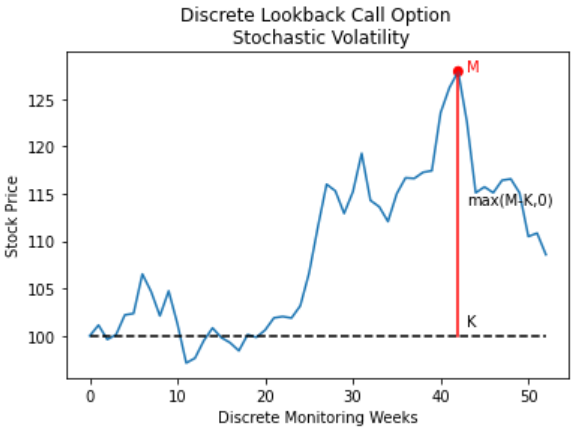
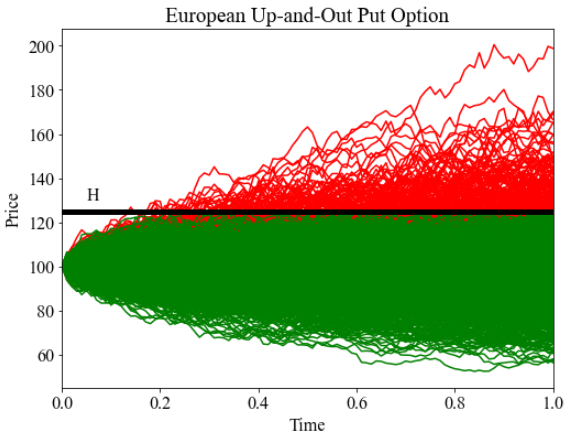
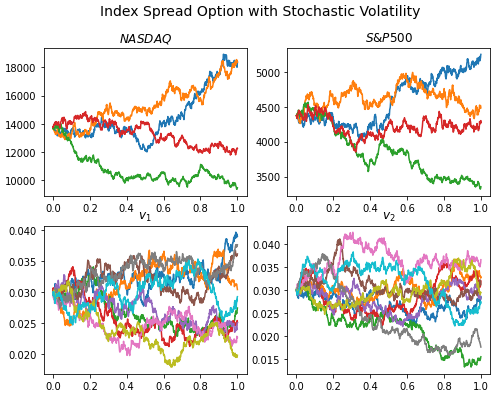
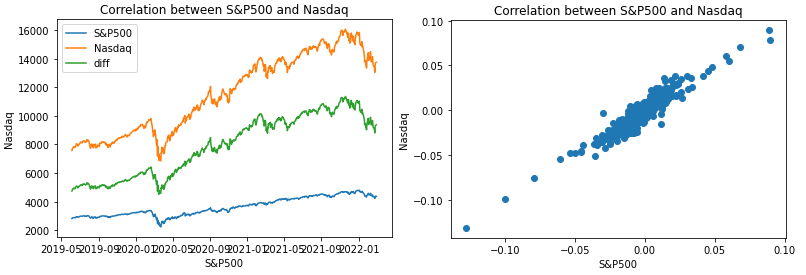
In this tutorial we are pricing a discretely monitored lookback call option with stochastic volatility. The option payoffs are dependent on the extreme values, maximum or minimum, of the underlying asset prices over a certain time period (lookback period). There are two standard lookback options: fixed strike and floating strike. Fixed strike discrete lookback option options pay the difference (if positive) between the max or min of a set of observations, over a lookback period of the asset price and the strike price at the maturity date.

There is no analytical solution for the price of European fixed strike lookback call options with discrete fixings and stochastic volatility under Heston model. However there is a simple analytical formula for the price of a continuously monitored (fixing) fixed strike lookback call with constant volatility.

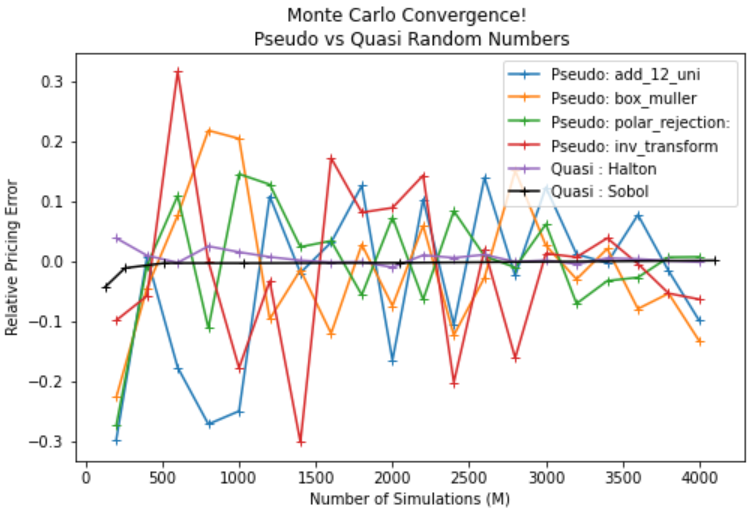
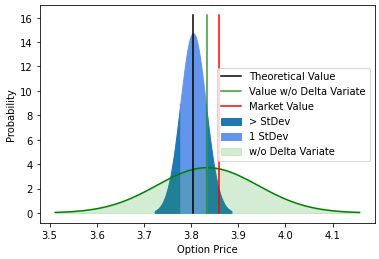
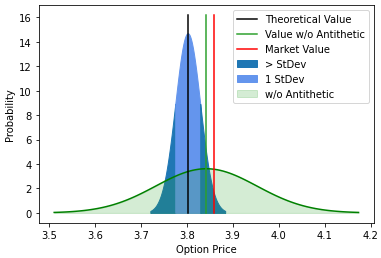
We will use a combination of Monte Carlo Variance Reduction techniques such as antithetic and control variate methods to reduce the standard error of our simulation. We use the analytical solution for a continuously monitored fixed strike lookback call option to calculate control variates based on delta, gamma and vega sensitivities.

In this tutorial we will be pricing an Average Price Option (APO) otherwise commonly referred to as an Asian Option. We will be pricing a bespoke OTC electricity average rate option in the Australian Electricity Market.

Electricity Average Rate Options in Australia / NZ Energy Markets are settled against the final futures prices. As futures are settled against the arithmetic average of the wholesale energy market price. Therefore final futures prices converge on the arithmetic average of wholesale electricity price. This essentially means listed ASX energy average rate options can be priced using blackscholes until the end of the quarter.

However, to demonstrate pricing of and Average Rate Option, and make things more interesting we will be looking at an OTC Asian Option over Q123 with the underlying as the Q123 NSW futures contract. Let’s say the average rate option prices are determined by the average of teh (closing) daily futures prices across the Q123 period.

In pricing complex or exotic path dependent options, a popular product is the barrier option. These are standard European option expiration style options, however the options cease to exist or only comes into existence if the underlying price crosses a pretermined barrier level. 

One of the main benefits of Monte Carlo simulations is to price options under multiple factors. By this I refer to multiple underlying asset prices or stochastic volatility or even changing interest rates. In this tutorial we will explore the pricing of a European Spread Call Option on the difference between two stock indices following a more general stochastic process. The SDE’s will be have stochastic volatility as described by the Heston Model (1993):

Trading Hypothesis: If Interest Rates Rise, Technology Companies valuations will be impacted worse than the broader stock market.
How can I benefit?

Today we look at how combining variance reduction methods like antithetic, delta and gamma-based control variates can help to substantially reduce the standard error around your theoretical option price during monte carlo simulations.

In this tutorial we will investigate ways we can reduce the variance of results from a Monte Carlo simulation method when valuing financial derivatives by using Delta-based control variates.

In this tutorial we will investigate ways we can reduce the variance of results from a Monte Carlo simulation method when valuing financial derivatives.